Deep Learning Study (2) _퍼셉트론

1. Perceptron Algorithm _퍼셉트론 알고리즘

 

** 일단 퍼셉트론은 다수의 신호를 입력으로 받아 하나의 신호를 출력한다.

 

퍼셉트론의 예

그림의 원을 뉴런 혹은 노드라고 부른다. 각각 고유한 가중치가 곱해집니다.(w1x2, w2x2) 뉴런에서 보내온 신호의 총합이 정해진 한계를 넘어설 때만 1을 출력합니다. 이 한계를 임계값(theta)로 나타낸다. 

 

y = 0 (w1x1 + w2x2 <= theta)

y = 1 (w1x1 + w2x2 > theta)

 

 

퍼셉트론으로는 AND 게이트, NAND 게이트, OR 게이트 모두 만들 수 있다.

 

위의 식은 수정될 수있다.

 

theta를 -b(bias, 편향)으로 치환하면 식은 수정된다.

 

 

y = 0 (b + w1x1 + w2x2 <= 0)

y = 1 (b + w1x1 + w2x2 > 0)

 

기존의 식에 편향을 더해준 값이 0을 넘으면 1, 넘지 못하면 0인 식으로 변화가 가능하다.

 

1_1. 퍼셉트론의 한계

XOR 게이트는 베타적 논리합입니다.

퍼셉트론은 직선 하나로 나눈 영역만 표현할 수 있다는 한계가 있습니다.

곡선의 영역, 비선형 영역은 표현할 수가 없습니다.

 

w1,w2는 각 입력 신호가 결과에 주는 영향력(중요도)을 조절하는 매개변수고, 편향은 뉴런이 얼마나 쉽게 활성화(결과로 1을 출력)하느냐를 조정하는 매개변수입니다. 예를 들어, b가 -0.1이면 각 입력 신호에 가중치를 곱한 값들의 합이 0.1을 초과할 때만 뉴런이 활성화합니다. 반면 b가 -20.0이면 각 입력 신호에 가중치를 곱한 값들의 합이 20.0을 넘지 않으면 뉴런은 활성화하지 않습니다. 한편 w1과 w2는 '가중치'로 b는 '편향'으로 구별하기도 합니다만 문맥에 따라 셋 모두를 '가중치'라고 할 때도 있습니다.

 

편향의 값이 중요하다.

 

 

2. Multi-layer Perceptron _다층 퍼셉트론

 

다층 퍼셉트론

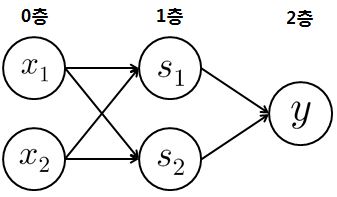
다층  퍼셉트론은 기존의 게이트 조합이 가능하다.

 

* 퍼셉트론의 한계는 정확히 말하면 "단층 퍼셉트론으로는 XOR 게이트를 표현할 수 없다" 또는 "단층 퍼셉트론으로는 비선형 영역을 분리할 수 없다."가 됩니다. 

 

 

x1	x2	s1	s2	y
0	0	1	0	0
1	0	1	1	1
0	1	1	1	1
1	1	0	1	0

 

1. 0층의 두 뉴런이 입력 신호를 받아 1층의 뉴런으로 신호를 보낸다.

2. 1층의 뉴런이 2층의 뉴런으로 신호를 보내고, 2층의 뉴런은 이 입력 신호를 바탕으로 y를 출력한다.